Using material advances in chalcogenide glasses to improve imaging lenses in the 8-14 μm waveband
Article shared under SPIE's Green Open Access Policy. Available here.
J. Verplancke, N. Schuster, J.W. Franks
ABSTRACT
Changes in the position of best focus over temperature are a major source of contrast degradation in the long-wave infrared. The prime sources of this focus shift are the difference between thermal expansion coefficients of lens material and housing material, and the change in refractive index over temperature ∂n/∂T. These parameters, combined with the limited depth of focus when using lenses for uncooled detectors, can rapidly degrade performance with changing temperature. First-order paraxial calculations to model these changes are discussed, with a demonstration of its application to single-element imaging systems. The model is then expanded to include two-element systems where both elements are made of the same optical material, or the more general case where different materials are combined. It is shown how a chalcogenide glasses are well suited for athermalization, and how a combination of material choice and optical prescription can lead to an improved passive optical athermalization scheme, i.e. stable performance over temperature with no moving components. The limits of the used model are discussed and examples given for various focal lengths.
Keywords: chalcogenide, optical athermalization, GASIR, LWIR, germanium, optical design, thermal infrared, SWaP-C
1. INTRODUCTION
Athermalization of optics is a key technology in the long-wave infrared and aims to compensate for changes in focus position over temperature. This thermally-driven movement of focal plane position is caused by changes in refractive index over temperature, differences between coefficients of thermal expansion (CTE) of optical components and their housing, and a limited depth of focus caused by the need for fast f-numbers in the uncooled long-wave infrared1.
Several ways exist to achieve athermalized performance1,2,3. One conceptually easy, but not cost-effective, way of maintaining focus over temperature is by using an active compensation mechanism; i.e. a motorized stepper that varies the distance between the lens and the focal plane based on an autofocus routine or a look-up table. While this technique is widely used for zoom lenses, it is an expensive solution for maintaining focus over temperature in fixed-focus configurations.
Passive focus compensation schemes rely on exploiting material properties as well as the geometry of an optical system to achieve athermalization. In its conceptually simplest incarnation, a high-expansion material moves the objective opposite to the direction of focal plane drift, thus maintaining proper contrast over a given temperature range. Most commonly, plastics are used for this purpose. In more advanced applications, where size and weight are critical aspects of a design, multi-element systems can be designed in such a way that the net effect of all thermal aberrations is almost zero. Consequently, the need for any moving components is removed and athermalization is achieved purely optically.
In this paper, we examine the athermalization of singlet as well as doublet lenses. Different focal length systems, representing different optical lay-outs, will be compared and their athermalization scheme discussed. Special attention will be devoted to material choice and how this influences thermal performance.
2. THERMAL ABERRATIONS AND THIN LENS APPROXIMATIONS
A first-order, thin-lens approximation of the total focus movement Δs over temperature ΔT of a lens in its housing can be written as4
![]()
where αH is the CTE of the housing material (commonly aluminum with αH = 23·10-6 K-1), f is the nominal system focal length and γT is the thermo-optical constant, defined as
![]()
Here, n denotes the refractive index at a given temperature and wavelength, and αL refers to the CTE of the lens material.
To quantify what athermalization means in practice, we consider the monochromatic depth of focus as defined by the so-called Rayleigh λ/4 criterion. This defines the maximum allowable focal plane drift as 2·λ·RF². Here, RF is the radiometric f-number² defined as 1/2𝑛sin𝜃, with n the image space refractive index and θ the cone angle in image space for an object at infinity. For practical lenses in the uncooled long-wave infrared, this yields a typical depth of focus of ± 20 – 40 μm.
The aim of any athermalization mechanism is to maximize the working temperature range ΔT, which by combining equation 1 with the Rayleigh criterion can be written as
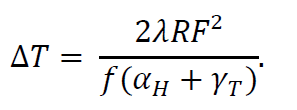
It can be seen that there are five parameters that influence the working temperature range of a lens. Of these, the wavelength λ, f-number RF and focal length f are generally fixed by the specification, though it is useful to be aware of their impact on athermalization. The biggest freedom the optical designer thus has to maximize ΔT, is by minimizing the sum of αH and γT.
Conceptually, the easiest way to athermalize a lens is by compensating mechanically for the change in best focal plane position. In equation 3, this implies changing the effective housing material expansion coefficient αH to closer match -γT. A high-expansion coefficient material such as certain types of plastic can be used to achieve this, with the effective expansion coefficient αH,eff then approximated by
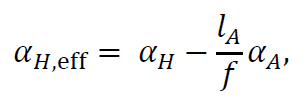
with lA the length of the athermalization mechanism and αA its coefficient of thermal expansion. The details behind this approach will not be further elaborated upon, for this we refer to the work of Schuster et al³.
3. MATERIALS
Historically, germanium has been a go-to material in the infrared due to its high refractive index, allowing more modest lens shapes without compromising optical quality. In addition, its crystalline structure confers some advantageous mechanical properties when compared to amorphous materials such as glasses, including high hardness for improved environmental resistance.
When considering thermal aspects, however, germanium has a number of undesirable properties. Firstly, its CTE differs significantly from that of aluminum, a popular housing material because it is easy to machine and has low cost. Upon significant temperature change, a germanium lens can undergo potentially destructive compression forces if the corresponding housing diameter has not been chosen appropriately. This can be overcome by providing added clearance between lens and housing diameters, or by choosing a suitable housing material, but this respectively decreases the tolerance budget and increases cost.
Secondly, at elevated temperatures germanium has a tendency to become opaque to infrared radiation. Absorption can grow by over an order of magnitude over a temperature increase of 60 °C. In addition, the absorption coefficient is quite sensitive to impurities with the absorption increasing as resistivity decreases, although the temperature effect is mitigated with decreasing resistivity.
Thirdly, germanium suffers from a large change in refractive index over temperature or ∂n/∂T, contributing significantly to focus shift and overall performance drop (see also equation 2).
In this paper, we will use germanium as a basis of comparison for the considered chalcogenide glasses as well as show how combinations of these materials can be used to achieve athermalization. Umicore Electro-Optical Materials manufactures both GASIR®1 and GASIR®5, two types of chalcogenide glass with the latter having the same composition as IG6, IRG26 and AMTIR-2.
Table 1: Material properties for the glasses used in this paper5. Note that Δn/ΔT represents the total index change over temperature, rather than the local derivative. Values are with respect to room temperature unless otherwise indicated.
| Germanium | GASIR®1 | GASIR®5 | |
| Refractive index at 10 μm | 4.0043 | 2.4944 | 2.7769 |
| Abbe number from 8 – 12 μm | 783 | 119 | 160 |
| Coefficient of thermal expansion (·10-6 K-1) | 5.70 | 17.0 | 23.5 |
| Δn/ΔT at 80 °C (·10-6 K-1) | 416 | 60.40 | 40.80 |
| Thermo-optical constant (·10-6 K-1) | 133 | 23.5 | 2.26 |
A comparison between these materials immediately reveals some interesting properties (Table 1). Germanium, with its high refractive index and low dispersion, often leads to designs with modest shapes and a reduced need for color correction. In chalcogenide elements, chromatic aberrations need to be corrected through the use of diffractive surfaces6, which can be molded directly onto the optical surface. When looking at thermal properties, we see that both GASIR®1 and GASIR®5 show much smaller index change over temperature as well as having CTEs that closely match that of aluminum. The net effect of these is that the thermo-optical constant is much closer to -αH in chalcogenide glasses than in germanium, leading to superior thermal performance as will be shown below.
4. SINGLE-ELEMENT DESIGNS
The ramifications of equation 1 can most easily be seen with a singlet design, as only one material needs to be considered and there is no spacing between lens elements to be taken into account. The section below illustrates the case for a short-focal length, single-element design.
The requirement for this design is a 90° horizontal field of view (HFoV) with a qVGA (320x240) 17 μm detector, with an aperture of f/1.33. Both solutions presented feature a similar back focal length (for shutter clearance) and optical lay-out with a positive meniscus with its convex side facing the detector (Table 2). Design A uses an aspheric germanium lens, whereas design B uses an aspheric lens made of the chalcogenide glass GASIR®5.
Using the material data listed in Table 1, design A’s performance seems likely to undergo a larger drop over temperature than design B. Indeed, when calculating Δs as per equation 1, we see that design B shows very little predicted focus drift at ±5 μm. By contrast, the ideal focal position in design A moves by ±35 μm.
Table 2: Lay-out and performance comparison of single-element designs in germanium and GASIR®5. See text for further detail.
The nominal performance of this germanium design surpasses that of the GASIR®5 design. This is largely thanks to its higher refractive index, allowing higher power and leaving more freedom to correct aberrations. The average MTF over field at the detector’s Nyquist limit drops by a modest 15% at most, whereas the GASIR®5 lens shows a spread on the order of 20% (also depending on the position of best focus). Other performance criteria such as distortion and relative illumination were similar between the designs (data not shown).
The advantages of design B compared to design A become apparent when looking at thermal behavior. When plotting the on-axis MTF in function of temperature, it can be seen that design B maintains essentially constant performance. This can be explained by the movement of the focal plane over temperature: while the allowable defocus is ±35 μm as per equation 3, design A shows a thermal focus shift of ±34 μm at the temperature extremes. By contrast, design B has a thermal drift of only ± 5 μm, corresponding to the analytical calculations made above.
This example illustrates that germanium lenses require focus compensation mechanisms for all but the shortest focal lengths and smallest apertures, or narrow operating temperature ranges.
5. WIDE-ANGLE DOUBLET DESIGN
To overcome the limitations of a single-element design, often two-element designs are needed to achieve the requirements for performance, size, weight and cost7. In addition to using these additional degrees of freedom to improve performance at a single temperature, a careful combination of materials and optical prescriptions can be used to minimize thermal aberrations.
For a two-element design, the thermo-optical constant can be shown to be a weighted contribution of both lenses and their separation:
![]()
Where γi and f i denote the thermo-optical constant and focal length of element i in the optical assembly, d is the separation between both lenses and αH is the coefficient of thermal expansion of the housing material. Note that this equation is again derived from paraxial optics assuming thin lenses, but that, contrary to most popular derivations, the separation between both lenses is taken into account. Given that the system focal length is generally a fixed requirement, a two-element system with different lens materials thus affords four extra variables and three extra degrees of freedom to set αH + γT = 0.
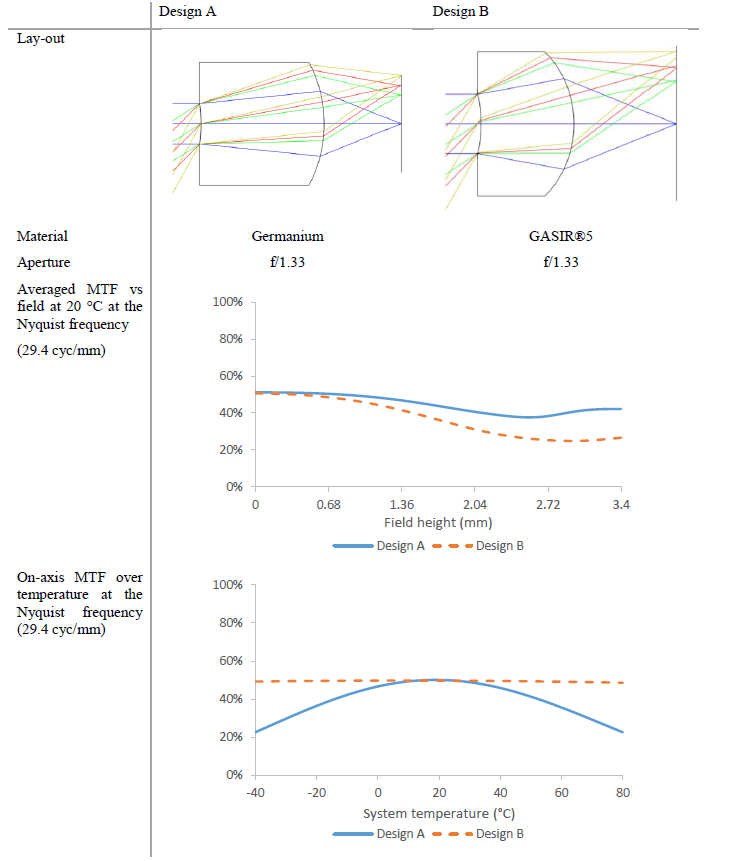
We examine the case of a short focal length doublet design with a requirement for a 90° HFoV with a 12 μm pixel pitch VGA (640x480) detector (Table 3). The desired operating temperature range is -40 °C to +80 °C. Constraints on minimum clearance between the lens and the detector necessitate the use of an inverse telephoto design.
In order to achieve a high (negative) power front lens without resorting to excessively steep curvatures, germanium was chosen as the lens material. Though this choice imposes some limitations, it is possible to minimize the thermal impact by optimizing for appropriate values of f1, f2, γ2 and d.
In this particular case, we have f = 4.9 mm (taking into account distortion) and γ1 = 133·10-6 K-1. For the second element, we select GASIR®5 as the lens material, which has a thermo-optical constant of 2.26·10-6 K-1. After optimization, we arrive at element focal lengths f1 = - 13.7 mm and f2 = 7.4 mm, with separation distance d 9.8 mm.
Inserting these values into equation 5 above, we find a system thermo-optical constant of 25.5·10-6 K-1. While this differs somewhat from the opposite of the housing CTE of -23·10-6 K-1, the subsequent focus drift is relatively low due to the short focal length, with a calculated defocus of ±14 μm at the extremes compared to room temperature. This matches the predictions of the OpticStudio optical design software, which shows a drift of ± 16 μm. This is well within the allowable defocus range of ±25 μm as defined by the Rayleigh criterion, hence no mechanical athermalization mechanism is needed.
6. MEDIUM FIELD OF VIEW DOUBLET DESIGNS
We define medium field of view lenses as having a field of view between 18 and 24 degrees. These focal lengths are of particular interest due to the fact that, in combination with commonly available detector formats, they approach the field of view of the human eye. This allows for an intuitive display of the captured information to the user.
Table 3: Lay-out and performance of a germanium + GASIR®5 doublet. Note the smooth thermal performance, which exceeds that of a germanium singlet even though the latter has a lower focal length (see Table 2). See text for further detail.
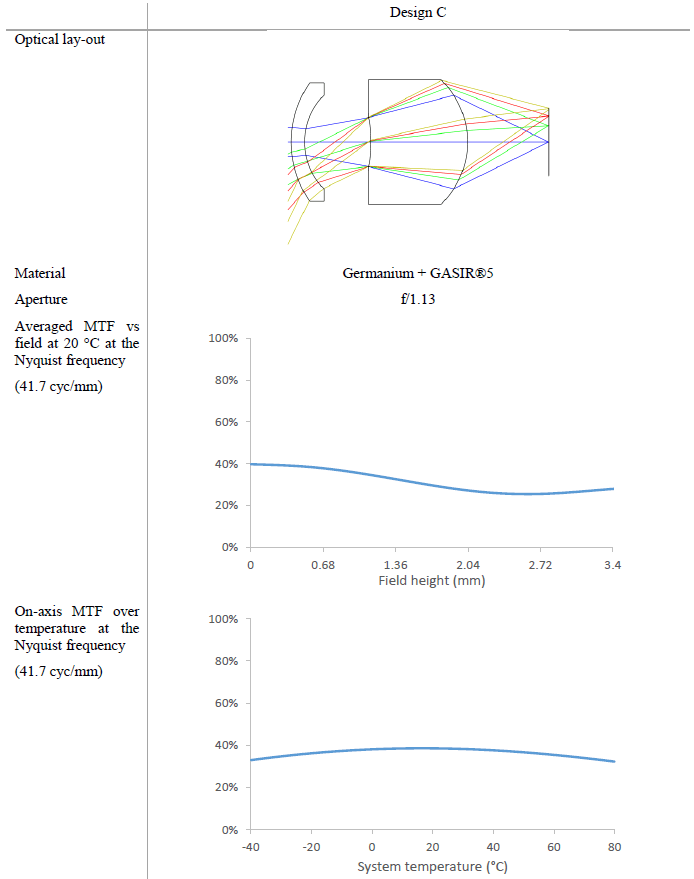
Table 4: Lay-out and performance comparison of two medium field of view designs. See text for further detail.
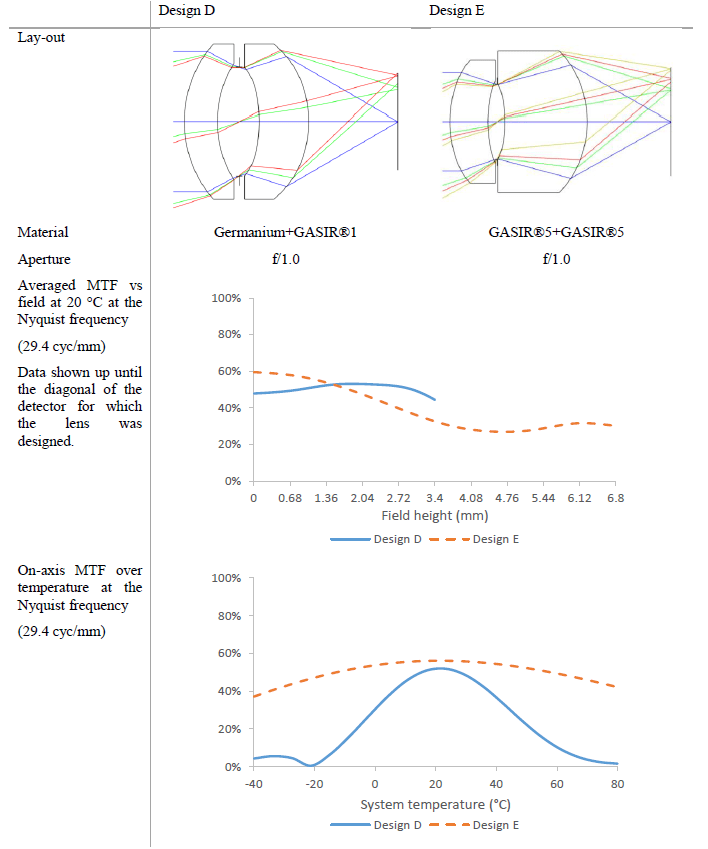
In this range of focal lengths, thermal aberrations start to become more prevalent as the focal length factor in equation 3 comes to dominate. The comparison below contrasts two 13 mm doublet designs. Low distortion and a fast, f/1.0 aperture are required, as well as athermal performance from -40 °C to +80 °C.
Both designs are variations on an Aplanat design, with each cemented doublet replaced with a single lens. In both layouts, power is distributed around the stop in a similar way (Table 4). In design D, the lens materials are germanium and GASIR®1, respectively, whereas in design E, both lenses are made of GASIR®5.
Basing ourselves on equation 5, design D shows a predicted focus drift of ±70 μm at the considered temperature extremes, whereas the total focal drift in design E is ±16 μm, compared to an allowable defocus of ±20 μm.
In terms of nominal performance at room temperature there are already some marked differences, some of which can be attributed to differences in degrees of freedom: though both lenses operate at f/1.0, the maximal field of view is on the order of twice as large in the GASIR®5+GASIR®5 design. Design D is shorter than design E, but suffers a larger illumination drop at similar field heights (data not shown). Both designs show low distortion, as can be expected from their layout.
The total focus drift as predicted by the OpticStudio software is ±80 μm for design D and ±19 μm for design E. While the order of magnitude of the change in focal plane over temperature is correct for design D, the deviation of the exact value from the predicted value above can be explained by a violation of the assumptions upon which our previous derivations are based. Nonetheless, the results show that the germanium-GASIR®1 design D thus requires a mechanical athermalization mechanism, whereas the all-GASIR®5 design E allows for passive optical athermalization without moving components.
This example illustrates the power of using lens materials with a low thermo-optical constant. Through the choice of GASIR®5 rather than a less suitable material, performance in terms of maximal field angle and temperature range has been increased, whilst simultaneously reducing the total number of components and thereby reducing cost and weight.
7. NARROW FIELD OF VIEW, LONG FOCAL LENGTH DESIGNS
The importance of a careful material choice and subsequent optimization for thermal performance becomes increasingly apparent with increasing focal length. By combining equations 1 and 5, we see that the change of focus over temperature scales is approximately quadratic with the focal length:
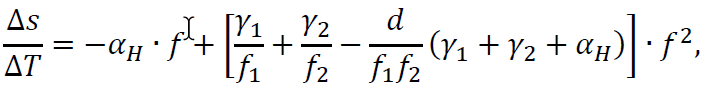
though it should of course be noted that d, f1 and f2 are related through the focal length and thus influence the exact shape of the Δs/ΔT curve. In the previous section, we elaborated upon the advantages of using GASIR®5 as a lens material and its superior thermal performance compared to a hybrid Ge+GASIR®1 design. Since the resulting design showed thermal focus drift at the edge of what was allowed per the Rayleigh λ/4 criterion, a different approach will be needed in this section to achieve passive optical athermalization.
To illustrate this approach, we therefore examine a long focal length design. The design requirement calls for an f/1.1 lens with an 8° HFoV when used with a VGA (640x480) 17 μm pixel pitch detector in a space envelope that is as small and as light as possible, as well as having an operating temperature range of +40 °C to -80 °C.
We compare a layout with two positive lenses in GASIR®5 (design F) to a layout with a positive front lens in GASIR®5 combined with a negative rear lens in germanium (design G). There are multiple advantages to the latter approach: Firstly, the optical back focal length can be increased while keeping the overall track length within acceptable bounds, albeit at the cost of a slight increase in tolerance sensitivity. Secondly, it can be seen from equation 1 that for f1 > 0 and f2 < 0 (and positive thermo-optical constants), the first two terms after the equals sign counteract each other. If the second element is made of a material with a large thermo-optical constant (like germanium), the sum of these two terms can even become negative, which aids in reducing αH + γT. The third term somewhat balances this effect, although its contribution is smaller because of the low power of the rear lens.
Table 5: Lay-out and performance comparison of two 75 mm f/1.1 lenses, design F being composed of two lenses made of GASIR®5, and design G being a GASIR®5+germanium hybrid. See text for further detail.
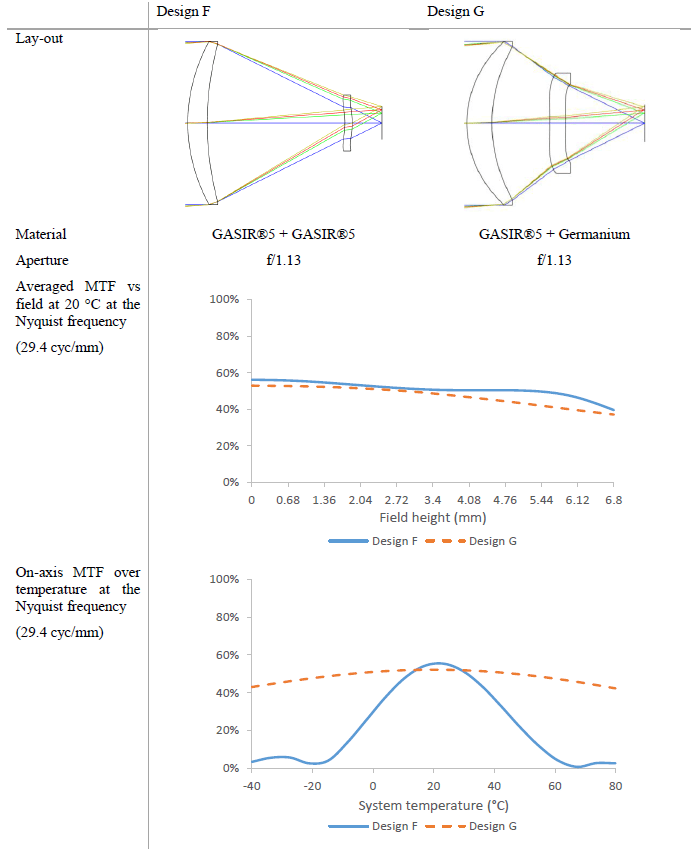
It should again be emphasized that all previously mentioned derivations rely on thin lens approximations. Given the fact that design G clearly deviates from these assumptions, the formulae can no longer be expected to be valid. In this case, we find a more accurate approximation for γT by setting d in equation 5 to be the distance between both elements’ principal planes, rather than their mechanical separation distance (which yielded results of sufficient accuracy in the previous sections).
The resulting effective thermo-optical constant γT in design G is -29.0·10-6 K-1, compared to the housing expansion coefficient αH of 23·10-6 K-1. This results in a predicted thermal focus drift of ±27 μm, compared to the allowable range of ±24 μm. By contrast, design F shows a thermo-optical constant of -6.4·10-6 K-1, which results in a predicted thermal defocus of ±75 μm.
Nominally, both lenses perform quite similarly to each other (Table 5). MTF over field is slightly higher in design F than in design G, however, design F is slightly longer with a reduced back focal length. Design G also has reduced distortion and a flatter relative illumination profile (data not shown).
The low system thermo-optical constant γT of design F can unfortunately not compensate for the focal length factor in the equation, thereby severely limiting its working temperature range. With a total movement range at the temperature extremes of ±98 μm, the averaged MTF drops to unusable levels. By contrast, the thermal defocus in design G is limited to ±7 μm at the extremes, compared to the allowable range of ±24 μm as mentioned above. This value is better than what was predicted analytically, and can be explained by deviations from paraxiality and thin lenses, and by differences in the assumed mounting mechanism. Indeed, the analytical equation assumes the (thin) lenses’ separation is governed only by expansion of the housing material. In reality, a mounting scheme can be chosen such that a (thick) lens’ expansion compensates for the change in separation due to housing expansion, if such a necessity should exist.
The lack of need for a mechanical focus compensation mechanism, together with the short track length afforded by the telephoto design, aids in reducing component count and complexity. As a result, the 75 mm f/1.1 lens of design G is one of the lightest lenses available on the market considering its large aperture.
8. CONCLUSION
Material properties have has a profound effect on thermal performance of any given optical design. For the simple case of a single thin lens, it can be shown that thermal focus drift is related to the difference in coefficients of thermal expansion between lens material and housing material, and the magnitude of the thermo-optical constant. Germanium suffers from a high thermo-optical constant, which implies that by design, a germanium lens will need some kind of thermal compensation mechanism to operate over even a modest temperature range. By contrast, chalcogenide glasses show a much smaller index change over temperature and are more compatible with aluminum, a common housing material. This allows for a decreased need to compensate for thermal defocus, leading to a reduction in size, weight and cost.
The magnitude of focal plane movement over temperature focus drift scales with the square of the focal length depending on element count and positioning. This means that even with low-drift materials, thermal defocus becomes an issue as the focal length increases. As longer-focal length lenses often contain two or more elements, however, the extra degrees of freedom can be used to minimize thermally-induced aberrations through balancing element powers with material properties. In doing so, the aim is to achieve a system thermo-optical constant approaching the opposite of the housing CTE. In this paper, we have demonstrated this approach for a wide range of focal lengths. The power of this method lies in the ability to reduce component count without reducing performance, especially for long focal length objectives where thermal effects are particularly strong.
It goes without saying that the formulae derived above are valid for the paraxial case from which they are derived. Violations of these assumptions will lead to deviations between predicted and actual values. Further divergence from the theory can be encountered when considering off-axis fields, nonlinearity of constants considered, and changing aberration balance with changing distance between two lenses. In these instances, the problem becomes intractable to solve analytically and numerical methods must be used to optimize the balance between nominal performance, athermalization and other design constraints.
Nonetheless, these formulae provide an indispensable starting point for correcting thermal aberrations whilst minimizing mechanical complexity and component count. Chalcogenide glasses have been shown to display various advantageous properties for use as a lens material, both when used alone or in combination with other materials.
REFERENCES
[1] Schuster, N. and Franks, J., “Depth of field in modern thermal imaging,” Proc. SPIE 9452, (2015)
[2] Schuster, N. and Franks, J., “Challenges, constraints and results of lens design for 17 micron-bolometer focal plane arrays in the 8-12 μm waveband,” Proc. SPIE 8012, (2011)
[3] Schuster, N. and Franks, J., “Passive athermalization of doublets in 8-13 micron waveband,” Proc. SPIE 9249, (2014)
[4] Riedl, M. J., “Optical Design Applying the Fundamentals”, SPIE PRESS TT84, Bellingham, WA, USA, 73-88 (2010)
[5] Umicore Electro-Optic Materials, “Materials,” Umicore, 01 March 2017, http://eom.umicore.com/en/infrared-optics/products/materials/ (13 March 2017)
[6] Ramsey, J.L. et al., “Experimental verification of the minimum number of diffractive zones for effective chromatic correction in the LWIR,” Proc. SPIE 9822, (2016)
[7] Bigwood, C. and Wood, J., “Two-element lenses for military applications,” Opt. Eng. 50(12), (2011)